Meta Regresi

Meta-regresi merupakan perluasan dari analisis sub kelompok. Berbeda dengan analisis sub kelompok yang hanya melihat karakteristik kategori, meta-regresi dapat menganalisis karakteristik kategori maupun kontinu. Selain itu, metode ini bisa menginvestigasi beberapa faktor sekaligus untuk melihat bagaimana faktor-faktor tersebut mempengaruhi efek intervensi. Namun, analisis ini membutuhkan jumlah studi yang cukup banyak, dan jika jumlah studi kurang dari sepuluh, meta-regresi sebaiknya tidak digunakan.

Meta Regresi vs Regresi Sederhana

Meta-regresi adalah metode analisis yang digunakan untuk memahami bagaimana karakteristik suatu studi mempengaruhi hasil intervensi dalam sebuah meta-analisis. Sederhananya, ini mirip dengan regresi biasa, di mana kita mencoba melihat hubungan antara satu atau lebih faktor dengan hasil tertentu. Dalam meta-regresi, hasil yang kita analisis biasanya berupa ukuran efek intervensi, seperti perbedaan rata-rata atau rasio risiko. Sementara itu, faktor yang kita teliti adalah karakteristik studi yang bisa mempengaruhi hasil intervensi, misalnya metode penelitian yang digunakan atau karakteristik peserta dalam studi tersebut, yang dapat juga disebut sebagai kovariat.

Ada beberapa perbedaan penting antara meta-regresi dan regresi biasa. Pertama, dalam meta-regresi, studi yang memiliki lebih banyak data dan hasil yang lebih akurat akan memberikan pengaruh lebih besar dibandingkan studi yang lebih kecil. Kedua, meta-regresi mempertimbangkan perbedaan yang tidak bisa dijelaskan hanya dengan faktor yang dianalisis, sehingga menggunakan pendekatan yang disebut “random effect model” untuk mengakomodasi variasi tersebut.

Hasil Meta Regresi

Koefisien regresi yang diperoleh dari analisis meta-regresi akan menjelaskan bagaimana variabel hasil (efek intervensi) berubah dengan peningkatan satu unit pada variabel penjelas (pengubah efek potensial/kovariat). Signifikansi statistik koefisien regresi merupakan pengujian apakah terdapat hubungan linear antara efek intervensi dan variabel penjelas. Koefisien regresi akan memperkirakan bagaimana efek intervensi di setiap sub kelompok berbeda dari sub kelompok referensi yang ditentukan. Nilai P dari setiap koefisien regresi akan menunjukkan kekuatan bukti terhadap hipotesis nol bahwa karakteristik tersebut tidak terkait dengan efek intervensi. Meta-regresi dapat dilakukan menggunakan makro “metareg” yang tersedia dalam paket statistik Stata, atau menggunakan paket “meta” atau “metafor” untuk R, serta paket dan software lainnya.

Meta Regresi pada R

Paket meta dalam R memiliki fungsi yang disebut metareg, yang digunakan untuk melakukan meta-regresi. Fungsi ini cukup sederhana karena hanya membutuhkan objek meta-analisis dari paket meta dan nama kovariat yang ingin dianalisis. Dalam contoh ini, kita ingin melihat apakah tahun publikasi suatu studi dapat digunakan untuk memprediksi ukuran efeknya. Untuk itu, kita akan menggunakan objek meta-analisis m.gen dengan data dummy bernama metabin.

Import Data & Membuat Meta Analisis

Sama seperti bagian sebelumnya pada Meta Analisis untuk data biner, data yang dibutuhkan sudah dimasukkan ke dalam excel (penjelasan lebih lengkap mengenai meta analisis data biner dapat dibuka pada bagian terkait).

Setelah mengunduh data dummy berjudul “metabin”, buka RStudio klik pilihan “Import Dataset” pada menu “Environment”. Kemudian, klik “From Excel”. Kemudian, klik “Browse” pada ujung kanan atas. Setelah itu, pilih file yang diinginkan. Lalu, klik “Import”.

  1. Install package: hanya perlu dilakukan satu kali saja, bila sudah pernah dilakukan, maka hanya perlu melakukan pemanggilan package

    install.package(c(“readx1”,"meta"))

  2. Pemanggilan package

    library(readx1) 
library(meta)

  3. Melakukan meta-analisis (dalam hal ini metabin: OR/RR)

    m.bin <- metabin( event.e = metabin$eventint,n.e = metabin$nint, event.c = metabin$eventcont,n.c = metabin$ncont, studlab = metabin$author, year = metabin$year, data = metabin, sm = "RR", method = "Inverse", common = TRUE, method.tau = "PM")

  4. Membuat rangkuman hasil

    summary(m.bin)
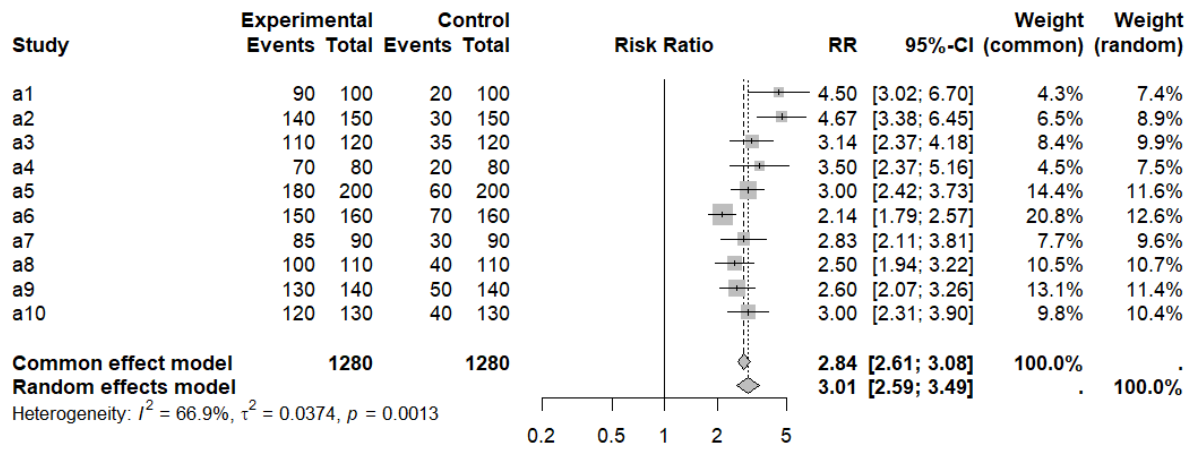
       RR           95%-CI %W(common) %W(random)
a1  4.5000 [3.0243; 6.6958]        4.3        7.4
a2  4.6667 [3.3789; 6.4453]        6.5        8.9
a3  3.1429 [2.3658; 4.1751]        8.4        9.9
a4  3.5000 [2.3733; 5.1616]        4.5        7.5
a5  3.0000 [2.4156; 3.7258]       14.4       11.6
a6  2.1429 [1.7895; 2.5660]       20.8       12.6
a7  2.8333 [2.1065; 3.8110]        7.7        9.6
a8  2.5000 [1.9389; 3.2235]       10.5       10.7
a9  2.6000 [2.0721; 3.2624]       13.1       11.4
a10 3.0000 [2.3072; 3.9008]        9.8       10.4

Number of studies: k = 10
Number of observations: o = 2560 (o.e = 1280, o.c = 1280)
Number of events: e = 1570

                         RR           95%-CI     z  p-value
Common effect model  2.8379 [2.6138; 3.0812] 24.86 < 0.0001
Random effects model 3.0061 [2.5900; 3.4891] 14.48 < 0.0001

Quantifying heterogeneity (with 95%-CIs):
 tau^2 = 0.0374 [0.0072; 0.1777]; tau = 0.1935 [0.0850; 0.4215]
 I^2 = 66.9% [35.5%; 83.0%]; H = 1.74 [1.25; 2.43]

Test of heterogeneity:
     Q d.f. p-value
 27.19    9  0.0013

Details of meta-analysis methods:
- Inverse variance method
- Paule-Mandel estimator for tau^2
- Q-Profile method for confidence interval of tau^2 and tau
- Calculation of I^2 based on Q

  1. Membuat forest plot

    forest(m.bin)

  2. Melakukan Meta Regresi

    Untungnya, dalam kumpulan data metreg, sudah ada variabel yang menyimpan informasi tahun publikasi setiap studi. Jadi, kita bisa langsung memanggilnya dengan perintah berikut:

    year <- m.bin$data$year

    Sekarang, kita sudah memiliki semua informasi yang dibutuhkan untuk menjalankan meta-regresi. Dalam fungsi metareg, kita cukup memasukkan nama objek meta-analisis kita, yaitu m.gen, sebagai argumen pertama. Lalu, kita tambahkan nama variabel prediktor yang ingin kita analisis, yaitu year, sebagai argumen kedua. Hasil dari meta-regresi ini akan kita simpan dan buka dalam objek bernama m.gen.reg.year dengan perintah berikut:

    m.gen.reg.year <- metareg(m.bin, ~year)
summary(m.gen.reg.year)
Mixed-Effects Model (k = 10; tau^2 estimator: PM)

  logLik  deviance       AIC       BIC      AICc   
  3.2964   14.2999   -0.5928    0.3150    3.4072   

tau^2 (estimated amount of residual heterogeneity):     0.0163 (SE = 0.0179)
tau (square root of estimated tau^2 value):             0.1276
I^2 (residual heterogeneity / unaccounted variability): 47.74%
H^2 (unaccounted variability / sampling variability):   1.91
R^2 (amount of heterogeneity accounted for):            56.50%

Test for Residual Heterogeneity:
QE(df = 8) = 18.1520, p-val = 0.0201

Test of Moderators (coefficient 2):
QM(df = 1) = 6.1396, p-val = 0.0132

Model Results:

         estimate       se     zval    pval    ci.lb     ci.ub    
intrcpt  111.1706  44.4289   2.5022  0.0123  24.0915  198.2497  * 
year      -0.0545   0.0220  -2.4778  0.0132  -0.0976   -0.0114  * 


Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Sekarang, kita telah menyelesaikan model dan mendapatkan beberapa hasil yang bisa kita pahami. Model ini menggunakan data dari 10 studi dan menghitung heterogenitas dengan metode Penalized Maximization (PM). Model campuran ini digunakan karena kita ingin melihat pengaruh dari efek tetap (fixed effect) dan efek acak (random effect) secara bersamaan. Heterogenitas residual, yang mengukur seberapa besar variabilitas yang belum dapat dijelaskan, ditemukan sebesar 0.0163, dengan standar error 0.0179. Ini menunjukkan bahwa ada sedikit variasi yang tidak bisa dijelaskan antara hasil studi. Kemudian, tau² (yang menunjukkan sebaran heterogenitas) memiliki nilai 0.1276, yang artinya ada sedikit perbedaan antara studi-studi dalam hal ukuran efeknya.

Angka I² sebesar 47.74% menunjukkan bahwa hampir setengah dari variasi yang ada disebabkan oleh perbedaan antar studi yang tidak dapat dijelaskan. Ini menunjukkan adanya heterogenitas moderat. Sedangkan, H² sebesar 1.91 menunjukkan bahwa setelah memperhitungkan heterogenitas, variasi dalam ukuran efek lebih besar 1.91 kali dibandingkan dengan variasi yang diharapkan hanya dari kesalahan pengambilan sampel. Namun, model ini juga menjelaskan lebih dari separuh heterogenitas yang ada, yaitu sebesar 56.50%, yang berarti bahwa moderator yang kita gunakan, dalam hal ini tahun publikasi, dapat menjelaskan lebih dari setengah perbedaan yang terlihat dalam ukuran efek.

Uji residual heterogenitas menunjukkan hasil yang signifikan dengan p-value 0.0201, yang berarti masih ada variasi yang tidak bisa dijelaskan setelah mempertimbangkan moderator. Sedangkan uji untuk moderator menunjukkan bahwa tahun publikasi memang mempengaruhi ukuran efek, dengan p-value 0.0132 yang signifikan. Untuk hasil model, kita menemukan bahwa interceptnya adalah 111.1706, yang bisa diartikan bahwa jika tahun adalah nol, ukuran efeknya adalah sekitar 111.17. Meskipun ini mungkin tidak realistis, ini berfungsi sebagai titik dasar.

Sedangkan untuk moderator tahun, koefisien yang didapat adalah -0.0545, yang berarti setiap penambahan tahun akan menurunkan ukuran efek sebesar 0.0545. Nilai p sebesar 0.0132 mengindikasikan bahwa pengaruh tahun terhadap ukuran efek ini signifikan. Kesimpulannya, model ini menunjukkan bahwa meskipun ada heterogenitas residual moderat (I² = 47.74%), lebih dari setengah heterogenitas ini (56.50%) dapat dijelaskan oleh tahun publikasi. Selain itu, baik intercept maupun pengaruh tahun terhadap ukuran efek menunjukkan hasil yang signifikan, dengan tren bahwa ukuran efek cenderung menurun seiring berjalannya waktu.

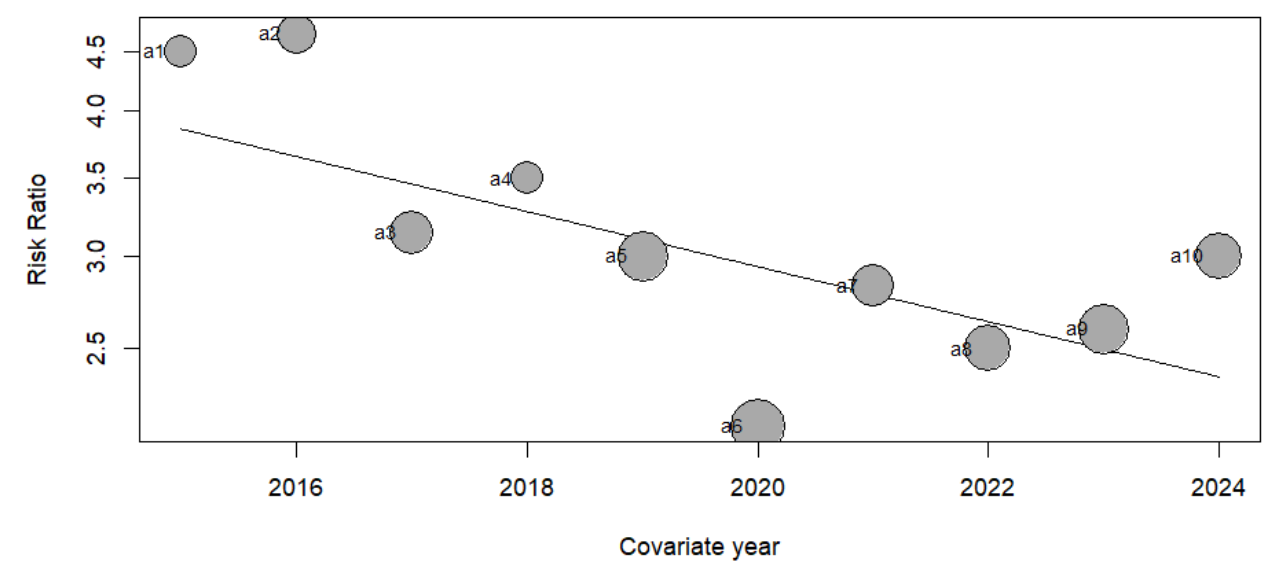
Visualisasi Meta Regresi

Paket meta dalam R juga memungkinkan kita untuk memvisualisasikan hasil meta-regresi dengan menggunakan fungsi bubble. Fungsi ini akan menghasilkan bubble plot, yang menampilkan kemiringan regresi yang diperkirakan serta ukuran efek dari masing-masing studi. Dalam plot ini, setiap studi direpresentasikan oleh gelembung dengan ukuran yang berbeda. Semakin besar gelembung, semakin besar bobot studi tersebut dalam analisis meta-regresi. Untuk membuat bubble plot, kita cukup memasukkan objek meta-regresi ke dalam fungsi bubble. Jika kita ingin menampilkan label studi pada plot, kita bisa menambahkan argumen studlab = TRUE.

bubble(m.gen.reg.year, studlab = TRUE)

Referensi

Harrer, M., Cuijpers, P., Furukawa, T. A., & Ebert, D. D. (2021). Doing Meta-Analysis with R. 9781003107347. https://doi.org/10.1201/9781003107347

Geissbühler, M., Hincapié, C.A., Aghlmandi, S., Zwahlen, M., Jüni, P. and da Costa, B.R., 2021. Most published meta-regression analyses based on aggregate data suffer from methodological pitfalls: a meta-epidemiological study. BMC Medical research methodology, 21(1), pp.1-9.

Chapter 10: Analysing data and undertaking meta-analyses. (2024). Cochrane.org. https://training.cochrane.org/handbook/current/chapter-10#_Ref180060159