Meta-Analisis Korelasi

Korelasi adalah ukuran asosiasi antara dua variabel. Perlu diperhatikan bahwa korelasi tidak menentukan hubungan sebab-akibat. Korelasi hanya mengukur kekuatan hubungan antara dua variabel. Di bagian ini, akan terdapat penjelasan mengenai koefisien korelasi Pearson dan Spearman. Meskipun begitu, masih terdapat banyak koefisien korelasi yang lain, seperti Kendall tau, Goodman-Kruskal gamma, dan lain-lain.

Korelasi

Pearson

Koefisien korelasi Pearson (r) adalah ukuran untuk asosiasi linear antara dua variabel. Jika diperlihatkan dalam representasi grafik, korelasi mengukur sejauh mana suatu variabel akan ikut meningkat atau menurun seiring dengan berubahnya nilai variabel lain. Nilai dari koefisien korelasi Pearson bervariasi mulai dari -1 hingga 1. Nilai yang mendekati 0 mengindikasikan rendah atau tidak adanya korelasi. Sebaliknya, nilai yang mendekati -1 atau 1 mengindikasikan tingginya korelasi.

Ada beberapa asumsi dalam menerapkan korelasi Pearson:

  1. hubungan linear antara variabel;

  2. variabel acak kontinu;

  3. variabel terdistribusi normal; dan

  4. variabel harus independen satu sama lain.

Koefisien korelasi Pearson dapat dihitung dengan

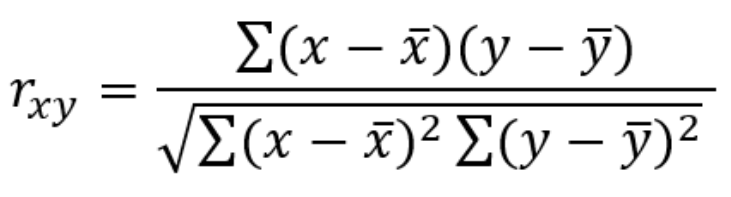
rxy=koefisien korelasi Pearson

x=nilai variabel 1

x= rerata nilai variabel 1

y=nilai variabel 2

y= rerata nilai variabel 1

Spearman

Korelasi orde peringkat Spearman (ρ) adalah ukuran asosiasi antara dua variabel. Ia berbeda dengan koefisien korelasi Pearson karena tidak berasumsi bahwa data yang digunakan berdistribusi normal. Selain itu, korelasi orde peringkat Spearman juga berbeda karena tidak menggunakan data mentah, tetapi diurutkan terlebih dahulu sebagai peringkat. Nilai dari korelasi orde peringkat Spearman memiliki aturan yang sama dengan koefisien korelasi Pearson.

Korelasi orde peringkat Spearman dapat dihitung dengan

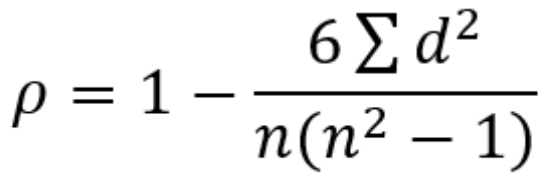
ρ=korelasi orde peringkat Spearman d=perbedaan peringkat variabel 1 dan variabel 2 dalam observasi yang sama n=jumlah data

Transformasi z Fisher

Untuk melakukan meta-analisis, koefisien korelasi biasanya ditransformasi terlebih dahulu menjadi nilai z Fisher. Pengubahan ini digunakan untuk memastikan korelasi terubah menjadi variabel yang berdistribusi normal. Dengan begitu, analisis menjadi lebih dapat dipercaya.

Transformasi z Fisher dapat dilakukan dengan

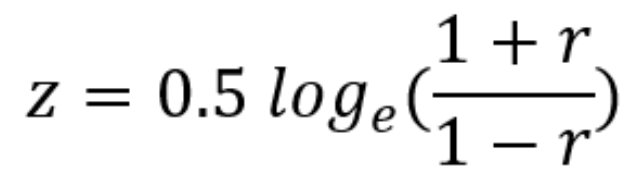
z=nilai z Fisher

r=koefisien korelasi

Meta-Analisis Korelasi di R

Seperti sudah dijelaskan pada bagian sebelumnya, analisis korelasi mengharuskan peneliti untuk mengubahnya menjadi nilai z Fisher terlebih dahulu. Kabar baiknya, program yang digunakan pada R sudah melakukan ini secara otomatis sehingga peneliti hanya perlu untuk memasukkan nilai korelasi dan jumlah sampel.

Data

Data yang dibutuhkan bisa dimasukkan ke dalam excel. Data memuat nama studi, koefisien korelasi, dan jumlah sampel. Data dummy dapat diakses pada Dummy Table

Setelah mengunduh data dummy, buka RStudio klik pilihan “Import Dataset” pada menu “Environment”. Kemudian, klik “From Excel”. Kemudian, klik “Browse” pada ujung kanan atas. Setelah itu, pilih file yang diinginkan. Lalu, klik “Import”

Meta-Analisis

  1. Install package terlebih dahulu

    install.packages(c(“dmetar”, “tidyverse”, “meta”))

  2. Pemanggilan package

    library(dmetar)
library(tidyverse)
library(meta)

  3. Meta-analisis

    m.cor <- metacor(cor = korelasi, n = jumlah sampel, studlab = studi, data = Dummy_Correlation, fixed = FALSE, random = TRUE, method.tau = "REML")

  4. Melihat hasil

    summary(m.cor)
         COR            95%-CI %W(common)
A 2011 0.2500 [-0.0908; 0.5384]       12.8
B 2015 0.2000 [-0.0830; 0.4531]       18.8
C 2013 0.3000 [ 0.0605; 0.5068]       24.8
D 2020 0.2700 [ 0.0374; 0.4748]       26.8
E 2025 0.2900 [-0.0039; 0.5378]       16.8

Number of studies: k = 5
Number of observations: o = 265

                       COR           95%-CI    z  p-value
Common effect model 0.2654 [0.1469; 0.3764] 4.30 < 0.0001

Quantifying heterogeneity:
 tau^2 = 0; tau = 0; I^2 = 0.0% [0.0%; 79.2%]; H = 1.00 [1.00; 2.19]

Test of heterogeneity:
    Q d.f. p-value
 0.35    4  0.9862

Details on meta-analytical method:
- Inverse variance method
- Restricted maximum-likelihood estimator for tau^2
- Fisher's z transformation of correlations

  1. Membuat forest plot

    forest(m.cor)

Referensi

Kirch W. Encyclopedia of public health. Dordrecht: Springer, Cop; 2008.

Schwarzer G, Carpenter JR, Rücker G. Meta-Analysis with R [Internet]. Use R! Cham: Springer International Publishing; 2015. Available from: https://link.springer.com/book/10.1007%2F978-3-319-21416-0

Yadolah Dodge. The concise encyclopedia of statistics. Germany ; London: Springer; 2008.