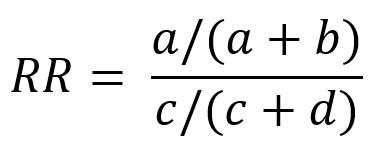Meta-Analisis Data Biner

Dalam dunia medis dan epidemiologi, Odds Ratio (OR) dan Risk Ratio (RR) merupakan dua ukuran statistik yang sering digunakan untuk mengevaluasi hubungan antara faktor risiko dan suatu kejadian. Kedua ukuran ini sangat penting dalam penelitian klinis, terutama dalam studi kohort dan studi kasus-kontrol. OR dan RR biasanya digunakan untuk data - data yang bersifat dikotomus. Data hasil dikotomis (biner) muncul ketika setiap peserta dalam penelitian memiliki salah satu dari dua kemungkinan hasil, seperti hidup atau mati, atau perbaikan klinis atau tidak.

Ketika membahas Odds Ratio (OR) dan Risk Ratio (RR) dalam analisis data dikotomis, kita selalu merujuk pada tabel 2×2. Tabel ini digunakan untuk menyajikan hubungan antara intervensi (atau paparan) dengan hasil klinis, sehingga memudahkan perhitungan ukuran efek.

Berikut adalah tampilan tabel 2×2 yang sering digunakan dalam analisis data klinis:

Sakit (kasus) Sehat Total
Terpapar a b a+b
Tidak Terpapar c d c+d

Definisi dan Konsep Dasar

Odds Ratio

Odds Ratio (OR) adalah ukuran yang membandingkan kemungkinan terjadi dan tidak terjadinya suatu peristiwa pada kelompok yang terpapar dengan tidak terpapar. OR sering digunakan dalam studi kasus-kontrol karena tidak bergantung pada insidensi penyakit dalam populasi. OR dapat dihitung menggunakan rumus berikut.

Risk Ratio

Risk Ratio (OR) adalah ukuran yang membandingkan kemungkinan terjadinya suatu peristiwa pada populasi terpapar dengan tidak terpapar. RR sering digunakan dalam studi kohort atau eksperimen. RR dapat dihitung menggunakan rumus berikut.

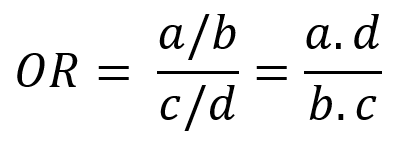
Meta-Analisis Data Biner di R

Data

Setelah mengunduh data dummy berjudul “metabin” atau dapat diakses pada halaman ini, buka RStudio klik pilihan “Import Dataset” pada menu “Environment”. Kemudian, klik “From Excel”. Kemudian, klik “Browse” pada ujung kanan atas. Setelah itu, pilih file yang diinginkan. Lalu, klik “Import”.

Melakukan Meta-Analisis

  1. Instalasi package hanya perlu dilakukan satu kali saja, bila sudah pernah dilakukan, maka hanya perlu melakukan pemanggilan package

    install.package(c(“readx1”,“meta”))

  2. Pemanggilan package

    library(readx1) 
library(meta)

  3. Melakukan meta-analisis

    m.bin <- metabin( event.e = metabin$eventint, n.e = metabin$nint, event.c = metabin$eventcont, n.c = metabin$ncont, studlab = metabin$author, year = metabin$year, data = metabin, sm = "RR", method = "Inverse", common = TRUE, method.tau = "PM")

  4. Membuat rangkuman hasil

    summary(m.bin)
       RR           95%-CI %W(common) %W(random)
a1  4.5000 [3.0243; 6.6958]        4.3        7.4
a2  4.6667 [3.3789; 6.4453]        6.5        8.9
a3  3.1429 [2.3658; 4.1751]        8.4        9.9
a4  3.5000 [2.3733; 5.1616]        4.5        7.5
a5  3.0000 [2.4156; 3.7258]       14.4       11.6
a6  2.1429 [1.7895; 2.5660]       20.8       12.6
a7  2.8333 [2.1065; 3.8110]        7.7        9.6
a8  2.5000 [1.9389; 3.2235]       10.5       10.7
a9  2.6000 [2.0721; 3.2624]       13.1       11.4
a10 3.0000 [2.3072; 3.9008]        9.8       10.4

Number of studies: k = 10
Number of observations: o = 2560 (o.e = 1280, o.c = 1280)
Number of events: e = 1570

                         RR           95%-CI     z  p-value
Common effect model  2.8379 [2.6138; 3.0812] 24.86 < 0.0001
Random effects model 3.0061 [2.5900; 3.4891] 14.48 < 0.0001

Quantifying heterogeneity (with 95%-CIs):
 tau^2 = 0.0374 [0.0072; 0.1777]; tau = 0.1935 [0.0850; 0.4215]
 I^2 = 66.9% [35.5%; 83.0%]; H = 1.74 [1.25; 2.43]

Test of heterogeneity:
     Q d.f. p-value
 27.19    9  0.0013

Details of meta-analysis methods:
- Inverse variance method
- Paule-Mandel estimator for tau^2
- Q-Profile method for confidence interval of tau^2 and tau
- Calculation of I^2 based on Q

  1. Membuat forest plot

    forest(m.bin)

Referensi

Alavi M, Hunt GE, Visentin DC, Watson R, Thapa DK, Cleary M. Using risk and odds ratios to assess effect size for meta‐analysis outcome measures. Journal of Advanced Nursing. 2020 Oct 13;76(12):3231–4.

Chapter 6: Choosing effect measures and computing estimates of effect [Internet]. Cochrane.org. 2023. Available from: https://training.cochrane.org/handbook/current/chapter-06#section-6-4