Meta-Analisis Kontinu

Pada setiap studi yang melibatkan nilai rata-rata dan standar deviasi, effect sizes yang diinginkan adalah (raw) mean difference dan standardized mean difference. Di bagian ini, akan terdapat penjelasan lebih lanjut mengenai mean difference dan standardized mean difference.

Mean Difference

Definisi

Ketika hasil penelitian dilaporkan dalam skala yang lazim digunakan dan dalam skala yang sama untuk setiap studi, meta analisis dapat dilakukan secara langsung pada mean difference atau yang lebih awam disebut raw mean difference. Keuntungan yang paling signifikan untuk metode ini adalah karena menggunakan skala yang berarti, hasil yang dihasilkan metode ini lebih mudah untuk disebarluaskan dan digunakan untuk pengguna yang lebih luas.

Standardized Mean Difference

Definisi

Jika pengukuran yang digunakan tidak terlalu lazim, penggunaan raw mean difference tidak terlalu direkomendasikan. Metode yang direkomendasikan merupakan standardized mean difference, dimana metode ini bisa digunakan untuk memfasilitasi studi-studi dengan instrumen penelitian yang berbeda untuk melihat hasil akhir (outcome) yang diinginkan. Dari studi-studi ini, dapat diambil standar deviasinya untuk membuat index yang dapat digunakan sebagai acuan perbandingan. Dua estimator SMD yang paling umum digunakan adalah Cohen’s d dan Hedges’ g.

Cohen’s d

Cohen’s d dihitung sebagai selisih antara rata-rata dua kelompok yang dibagi dengan standar deviasi gabungan (pooled standard deviation). Secara matematis, Cohen’s d direpresentasikan sebagai:

di=(yi1-yi0)/siP

di mana yi1 adalah rata-rata kelompok perlakuan, yi0 adalah rata-rata kelompok kontrol, dan siP adalah standar deviasi gabungan. Cohen’s d dapat mengalami bias, terutama ketika ukuran sampel kecil.

Hedges’ g

Hedges’ g adalah versi bias-corrected dari Cohen’s d. Metode ini menyesuaikan Cohen’s d dengan faktor koreksi untuk mengatasi bias akibat ukuran sampel yang kecil. Hedges’ g dihitung sebagai:

gᵢ = J(mᵢ) dᵢ

di mana J(mᵢ) adalah faktor koreksi, dan dᵢ adalah Cohen’s d. Hedges’ g dirancang untuk memberikan estimasi tak bias dari perbedaan rata-rata terstandarisasi, terutama saat menangani sampel berukuran kecil.

Perhitungan SMD

Untuk menghitung Standardized Mean Difference (SMD), ikuti langkah-langkah berikut:

Kumpulkan Data

Ambil data rata-rata (mean), standar deviasi (standard deviation), dan ukuran sampel dari setiap penelitian yang digunakan.
Hitung Cohen’s d atau Hedges’ g.

Untuk Cohen’s d, standar deviasi gabungan (pooled standard deviation) dihitung dengan rumus berikut:
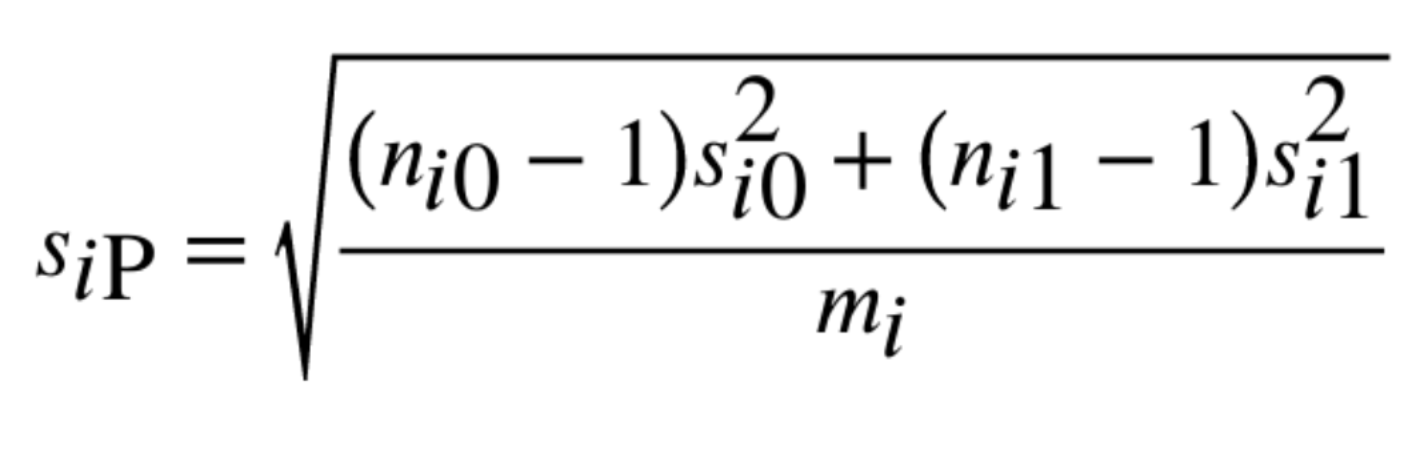
Lakukan Perhitungan untuk Setiap Studi

Ulangi langkah perhitungan ini untuk setiap studi yang disertakan dalam meta-analisis.

Tutorial R

Link Dummy Table: Dummy Table

Tutorial Meta-Analisis Mean Difference di R

Install paket meta (jalankan hanya sekali)
```
install.packages("meta")
```
Load paket meta
```
library(meta)
```

Memasukkan Data Studi dalam Data Frame

data_md <- data.frame( study = c("Studi 1", "Studi 2", "Studi 3"), mean_treat = c(85, 78, 90), sd_treat = c(10, 8, 15), n_treat = c(50, 40, 60), mean_control = c(80, 75, 85), sd_control = c(12, 9, 14), n_control = c(50, 40, 60))

Analisis Meta untuk Mean Difference (MD)

md_meta <- metacont( n.e = data_md$n_treat, mean.e = data_md$mean_treat, sd.e = data_md$sd_treat, n.c = data_md$n_control, mean.c = data_md$mean_control, sd.c = data_md$sd_control, studlab = data_md$study, sm = "MD", )

Menampilkan Hasil MD
```
summary(md_meta)
```

    MD             95%-CI %W(common) %W(random)
    Studi 1 5.0000 [ 0.6703;  9.3297]       32.9       32.9
    Studi 2 3.0000 [-0.7317;  6.7317]       44.3       44.3
    Studi 3 5.0000 [-0.1917; 10.1917]       22.9       22.9


    Number of studies: k = 3
    Number of observations: o = 300 (o.e = 150, o.c = 150)


                          MD           95%-CI    z p-value
    Common effect model  4.1148 [1.6323; 6.5974] 3.25  0.0012
    Random effects model 4.1148 [1.6323; 6.5974] 3.25  0.0012


    Quantifying heterogeneity (with 95%-CIs):
    tau^2 = 0 [0.0000; 48.2714]; tau = 0 [0.0000; 6.9478]
    I^2 = 0.0% [0.0%; 89.6%]; H = 1.00 [1.00; 3.10]


    Test of heterogeneity:
        Q d.f. p-value
    0.62    2  0.7353

Visualisasi Forest Plot

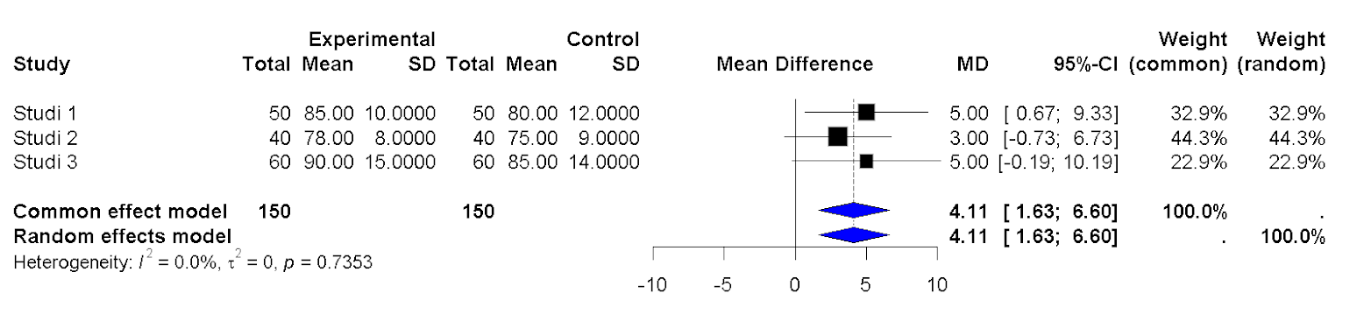
forest(md_meta, col.diamond = "blue", col.square = "black")

Tutorial Meta-Analisis Standardized Mean Difference di R

Install paket meta (jalankan hanya sekali)
```
install.packages("meta")
```
Load paket meta
```
library(meta)
```

Memasukkan Data Studi dalam Data Frame

data_md <- data.frame( study = c("Studi 1", "Studi 2", "Studi 3"), mean_treat = c(85, 78, 90), sd_treat = c(10, 8, 15), n_treat = c(50, 40, 60), mean_control = c(80, 75, 85), sd_control = c(12, 9, 14), n_control = c(50, 40, 60))

Analisis Meta untuk Standardized Mean Difference (SMD)

smd_meta <- metacont( n.e = data_md$n_treat, mean.e = data_md$mean_treat, sd.e = data_md$sd_treat, n.c = data_md$n_control, mean.c = data_md$mean_control, sd.c = data_md$sd_control, studlab = data_md$study, sm = "SMD", method.smd = "Hedges" )

Menampilkan Hasil SMD
```
summary(smd_meta)
```

           SMD            95%-CI %W(common) %W(random)
        Studi 1 0.4492 [ 0.0521; 0.8463]       33.1       33.1
        Studi 2 0.3489 [-0.0928; 0.7907]       26.7       26.7
        Studi 3 0.3424 [-0.0181; 0.7030]       40.2       40.2

    Number of studies: k = 3
    Number of observations: o = 300 (o.e = 150, o.c = 150)


                             SMD           95%-CI    z p-value
    Common effect model  0.3795 [0.1511; 0.6080] 3.26  0.0011
    Random effects model 0.3795 [0.1511; 0.6080] 3.26  0.0011


    Quantifying heterogeneity (with 95%-CIs):
    tau^2 = 0 [0.0000; 0.1007]; tau = 0 [0.0000; 0.3174]
    I^2 = 0.0% [0.0%; 89.6%]; H = 1.00 [1.00; 3.10]


    Test of heterogeneity:
        Q d.f. p-value
     0.18    2  0.9151

Visualisasi Forest Plot

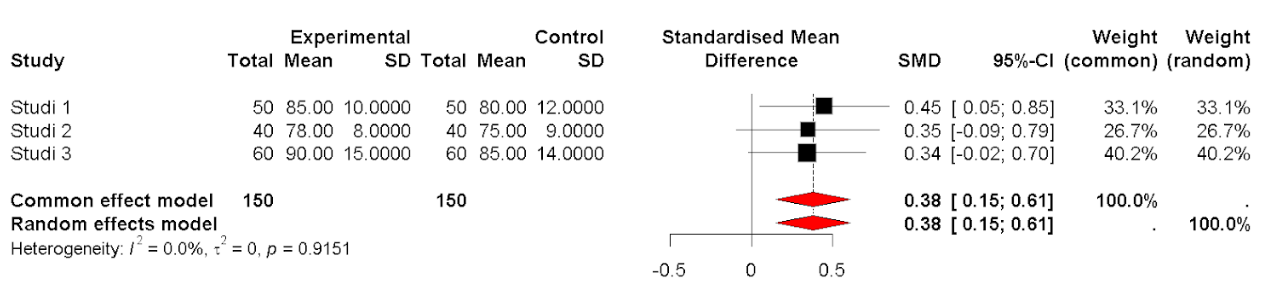
forest(smd_meta, col.diamond = "red", col.square = "black")

Referensi

Lin L, Aloe AM. Evaluation of various estimators for standardized mean difference in meta-analysis. Stat Med. 2021 Jan 30;40(2):403–26. doi:10.1002/sim.8781.